[텐서플로우로 시작하는 딥러닝 기초] Lec 04: Multi-variable Linear Regression

휴가 다녀와서 2주 동안 격리를 당하느라 거의 3주 만에 노트를 작성한다. 마침 친절하게도 강의 초반에 이전 강의들을 복습시켜줬다.

 

 

지금까지 가설과, 비용함수의 개념과 비용을 최소화시키는 방법 중 하나인 경사 하강법을 배웠다.

 

우리가 지금까지 배운 개념은 하나의 variable에 하나의 feature가 있다.

그런데 위와 같이 하나의 변수를 가지고 정확한 예측을 할 수 있을까? 가능할 수 도 있지만 그렇지 않은 경우가 더 많을 것이다.

그래서 우리는 둘 이상의 변수를 같은 예측치를 가지고 학습을 시켜야 할 것이다. 그래서 오늘 다중 선형 회귀(Multi-variable Linear Regression)를 배울 것이다.

 

위와 같이 다중 변수(x1, x2, x3)를 갖는 경우이다. 이렇게 되면 차원이 증가하는 모양일 것 같다. 이에 대한 Hypothesis는 아래와 같다.

각각의 변수에 각각의 가중치를 갖는다. Cost function은 아래와 같다.

변수가 늘어나는 만큼 가중치도 늘어난다. 그런데 변수가 3개가 아니라 더 많아지면 위와 같은 식으로 표현하기 매우 힘들것이다.

우웩..

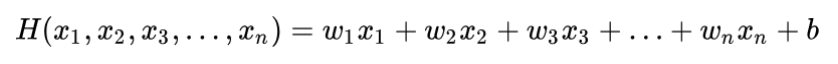
그럼 어떻게 하면 될까?? 아! 행렬의 곱으로 나타내면 되겠다!

좌측 Matrix의 column과 우측 Matrix의 row 수를 맞추는건 기본~

matrix는 어딜가나 있구나

아래처럼 instance(variables, feature의 data set)가 많은 경우에도

행렬의 곱으로 간단히 나타낼 수 있다.

 

이론상의 수식에서는 보통 계수인 W를 x앞에 쓰지만 matrix의 형태 Tensorflow에서 구현하기 때문에 XW로 쓴다.