[텐서플로우로 시작하는 딥러닝 기초] Lab 03: Linear Regression and How to minimize cost 를 TensorFlow 로 구현하기

저번 시간에 우리의 가설 함수는 H(x) = Wx. 원점을 지나는 함수로 simplified 하기로 했다. 아직은 Gradient descent를 배우는 단계이기 때문에. 그리고 Cost함수는 아래와 같다.

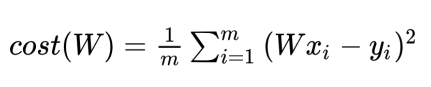
이 Cost 함수를 파이썬으로 구현해보자. (텐서플로우 없는 그냥 파이썬)

import numpy as np

#data 설정
X = np.array([1,2,3])
Y = np.array([1,2,3])

#cost 함수 정의
def cost_func(W, X, Y):
	c = 0
    for i in range(len(X)):
    	c += (W * X[i] - Y[i]) ** 2 #가설과 실제 데이터 차의 제곱의 합을
    return c / len(X) #평균내주기
    
for feed_W in np.linspace(-3, 5, num=15): #W값을 -3 부터 5까지 15조각으로 나누어 넣어보자
	curr_cost = cost_func(feed_W, X, Y) #현재의 cost
    print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))

출력

좌측이 -3부터 5까지의 W값이고 우측이 이에 따른 cost 값이다. 우리가 예상할 수 있는 대로 W=1일 때 cost가 0이 되는 모습이다.

cost함수는 우측의 그래프의 모습일 것이다.

 

이번에는 텐서플로우로 구현해보자.

import numpy as np
import tensorflow as tf

X = np.array([1, 2, 3])
Y = np.array([1, 2, 3])

def cost_func(W, X, Y):
	hypothesis = X * W
    return tf.reduce_mean(tf.square(hypothesis - Y)) 
    #tf.reduce_mean은 평균을 내는 함수라고 저번에 배웠다. reduce가 들어가는 이유는 tensor의 차원이 줄기 때문이다. tf.square는 인자를 제곱해주는 함수이다.
    
W_values = np.linspace(-3, 5, num=15) #W값에는 -3부터 5사이의 수를 균등하게 15번 쪼개서 넣을 것이다.

for feed_W in W_values:
	curr_cost = cost_func(feed_W, X, Y)
    print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))
	

출력

당연하게 같은 결과이다.

---

Gradient descent에서는 cost함수를 W로 미분한 뒤 이를 W에서 빼는 방식으로 W값을 찾아간다.

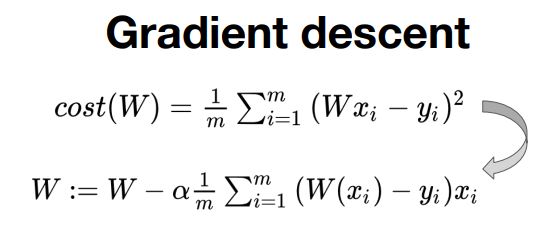
이를 텐서플로우로 아래와 같이 짠다.

alpha = 0.01 #learning rate는 보통 매우 작게 설정한다.
gradient = tf.reduce_mean(tf.multiply(tf.multiply(tf.multiply(W, X)-Y), X) #cost함수의 미분식
descent = W - tf.multiply(alpha, gradient) #미분한 식을 W에서 빼는 모습
W.assign(descent) #뺀 값을 W에 다시 할당

단순히 함수를 텐서플로우로 구현한 것이니, 텐서플로우에서 연산을 어떻게 명령하는지 보면 좋을 것 같다.

---

자 이제 다시 Gradient descent를 텐서플로우로 구현해보자.

import tensorflow as tf
import numpy

tf.random.set_seed(0)

x_data = [1, 2, 3, 4]
y_data = [1, 3, 5, 7]

W = tf.Variable(tf.random.normal([1], -100, 100)) #-100 부터 100사이 정규분포 난수

print(W)
for epoch in range(300): #300번 학습을 돌리자
    hypothesis = W * x_data
    cost = tf.reduce_mean(tf.square(hypothesis - y_data))

    alpha = 0.01
    gradient = tf.reduce_mean(tf.multiply(tf.multiply(W, x_data) - y_data, x_data))
    descent = W - tf.multiply(alpha, gradient)
    W.assign(descent)

    if epoch % 20 == 0:
        print('{:5} | {:10.4f} | {:10.6f}'.format(epoch, cost.numpy(), W.numpy()[0]))

사실 텐서플로우에는 Gradient descent를 수행하는 함수가 포함되어있다. 그치만 기초부터 쌓아간다 생각하고 일일이 코드를 짜보자. W에는  -100부터 100 사이의 정규분포 중 하나의 값을 받아서 시작해보자.

 

출력

이번에는 데이타셋이 원점을 지나는 직선위에 올라올 수 없음을 예상할 수 있었고 실제로 W값은 약 1.6666에서 멈추었다. 우리의 hypothesis가 bias를 제외한 함수였기 때문이다.