2020. 9. 3. 22:17ㆍ머신러닝
로지스틱 회귀/분류의 개념을 알아보는 시간이다. Logistic regression과 Linear regression의 차이는 무엇일지 궁금하다. 또한 분류라고 하니 이번에는 Unsupervised learning인가?라고 생각되는데 과연 그럴지 알아보자.

강의 목차. 이 강의는 스탠포드 Andrew Ng 교수님의 ML강의와 모두를 위한 딥러닝 강의의 김성훈 교수님의 자료를 토대로 설명한다고 한다.

Binary Classification은 예시들처럼 둘 중 하나로 분류가 된다. 그렇기 때문에 1 또는 0의 값을 갖는 학습 데이터가 쓰인다.
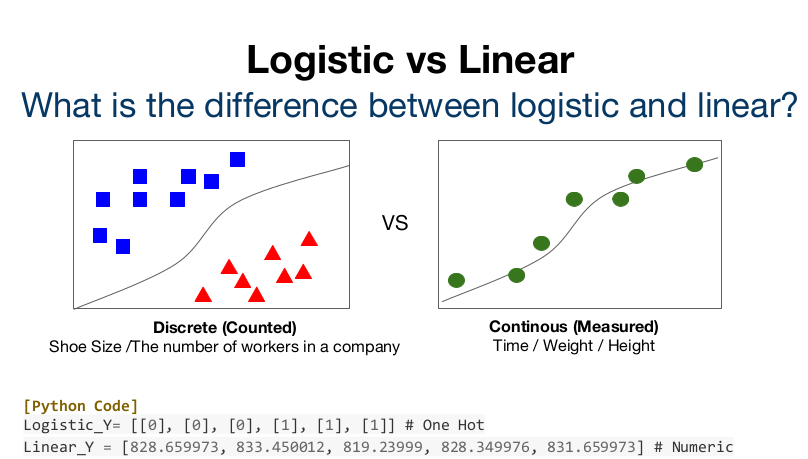
그렇다면 우리가 지금까지 배운 Linear regression과 Logistic regression의 차이는 우리가 원하는 출력에 있겠다.
Linear regression은 학습데이터를 바탕으로 test 데이터의 결과를 예상하는 것이고 Logistic regression은 0 또는 1의 학습 데이터를 바탕으로 test 데이터가 둘 중 어디에 더 가까운지를 찾아내는 것이겠지? 그래서 Logistic regression의 데이터들은 분리되어있고 셀 수 있지만 Linear regression의 데이터들은 연속적이라는 차이가 있다.

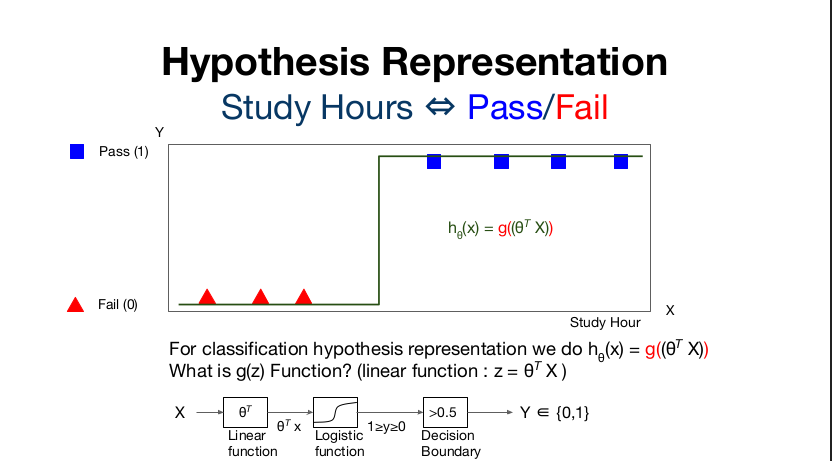
따라서 이전 강의에서 처럼 학습 시간에 따라 점수를 예상하는게 아니라 합격 여부를 예상하는 알고리즘을 원한다면 Linear regression을 적용할 수 없을 것이다. 입력 X에 대해 기존의 linear function(z = θX)의 결과를 도출하고 이를 Logistic function(g(z))의 형태로 0과 1 사이의 결과로 변형시킨 후 Decision boundary로 1과 0으로 나눈다는 것이라고 한다. 이때 logisitic function이 바로 아래의 Sigmoid (Logistic) function이다.
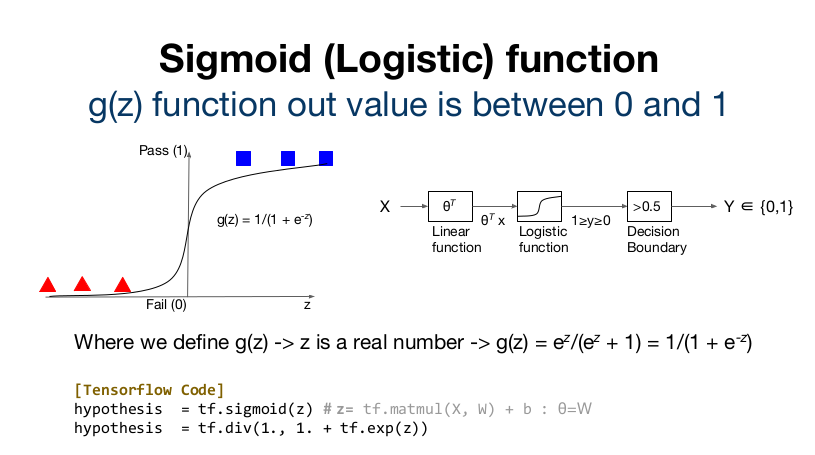
sigmoid function은 linear regression을 통해 얻은 z값을 지수로 갖는 Exponential을 이용해 z=0을 기준으로 급격히 분리되는 1과 0의 결과를 만든다. Tensorflow에서는 sigmoid함수를 지원하고 아래의 코드로 표현할 수 도 있다.
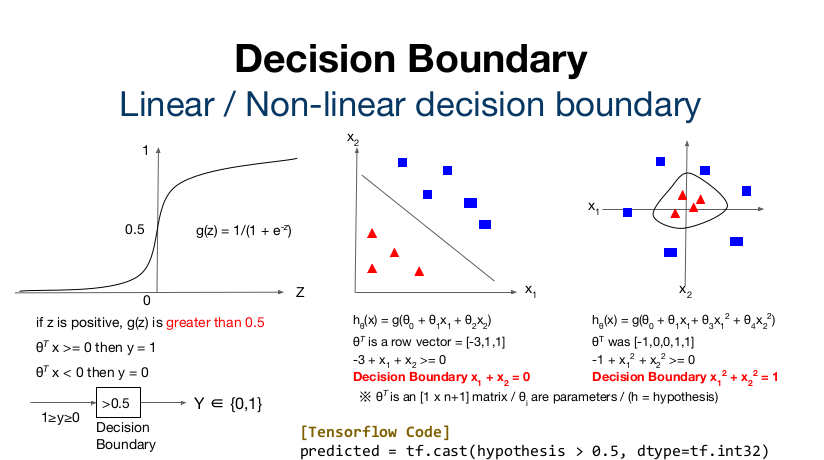
값을 1과 0으로 나누는 기준이 Decision Boundary 이다. 두 번째 그림의 Linear funcion에서 x1, x2의 합이 3 이상인지 아닌지에 따라 네모와 세모가 구분되는 것. 즉 Decision boundary는 x1 + x2 = 3이 되겠다. (사진에는 오타) 세 번째도 마찬가지로 x1^2 + x2^2 = 1이 decision boundary임을 알 수 있다.