2020. 10. 17. 19:36ㆍ머신러닝
20.10.14
너무 오랜만이다. 사실 중간에 자바 공부로 넘어갔다 오기도 했고 9월에 대대전술훈련과 10월 초에 종측 선발이 되어서 한동안 머신러닝 공부를 못했다. 오늘은 지금까지 배운 선형회귀와 로지스틱 회귀에 대해 복습하는 시간을 가진 후 머신러닝으로 복귀를 했다.
Logistic Regression: Linear Regression를 Classification에 사용할 때의 한계들을 수정하여 선형 가설을 Sigmoid 형태에 넣은 Hypothesis를 설정했다. 그리고 Local Minimum 문제를 피해 그에 맞는 log를 이용한 Cost Function을 만들었다. 이를 앞서 배운 경사하강법으로 Cost 값을 최소화시키는 Weight와 Bias를 찾는 것이다.
이미지가 잘 그려지지는 않는다. 그래서 sigmoid 함수가 어떻게 모양이 바뀌는지 봤다. 나는 분류를 위해서 Hypothesis가 0.5인 부분이 실제 데이터의 Label 값이 0에서 1로 바뀌는 곳에 위치해야 한다고 생각했다. 이것이 모델을 구하는 과정이라고 생각했는데, 사실 Weight값은 그 부분에서 변화를 일으키지 않는다. bias가 sigmoid를 이동시킨다. 나의 이런 생각들이 강의에서 설명하는 바와는 맞지 않는 것이 느껴진다. 중간에 설명이 부족한 부분이 있던가 내가 이해를 제대로 못했다는 것이다.
20.10.16
로지스틱 회귀에 대해 찾아보고 다른 글들도 뒤져보며 내가 어느 부분에서 잘못 개념을 잡았는지 찾고 있다.
먼저, 선형 회귀는 연속적인 데이터들의 특징을 잡아서 새로운 데이터의 값을 기존 데이터의 맥락에 맞추어 찾는 것이라면
(이진) 로지스틱 회귀는 각각의 특징을 가진 데이터들이 0 또는 1이라는 집단으로 나누어져 있을 때 그 두 집단의 경계를 찾아 새로운 데이터가 어느 집단에 속하는지를 예측하는 것이다. 즉 y 값이 discrete 하다는 것이다. 이러한 학습 데이터에 맞는 Hypothesis로 Sigmoid 함수를 이용한 것이고 이 Hypothesis로 나오는 결괏값은 1과 0 사이의 값이다. 그리고 decision boundary를 기준으로 1이냐 0이냐 라는 결과를 만든다.
Hypothesis를 Traning set에 맞추기 위해 Cost function을 생각해보자. 단순히 hypothesis와 y의 값의 차이를 통한 cost function은 더 이상 logistic regression에서는 사용 못한다. 그래서 Log를 이용해 우리의 입맛에 맞는 cost function을 만들었다.(looma1116.tistory.com/19?category=903335)
20.10.17
내가 막혔던 부분은 Lab 05-3 코드 실습 강의에서 아래의 그림들처럼 그룹을 구분하는 선을 그리는 모델이라는 점이었다.

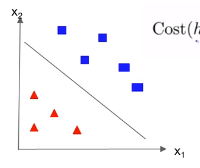
아니 도대체 시그모이드 함수로 Hypothesis를 만들고 Log를 이용해 Cost function을 만들어서 Gradient descent를 하는 건 알겠는데 저런 구분선은 어디서 튀어나온 거지? decision boundary라고는 했던 것 같은데 말이야. 어떤 과정을 통해 저렇게 시각화되고, 우리의 시그모이드는 어디로 간 거지?

그래서 생각을 했다. 앞서 로지스틱 회귀의 개념을 배울 때 하나의 x를 갖는 데이터들과 2차원 적인 sigmoid function을 적용시키는 모습을 봤다. 그런데 저 그림은 두 개의 x (feature)를 갖고 y (label)은 색으로 표현이 된다. 그럼 평면이 아니라 3차원으로 y축을 그려보자. Decision Boundary는 y=0.5인 평면이 되겠군 그렇다면 우리의 모델은 이런 모습이 아닐까?
(휴학을 하지 않고 3학년 1학기에 인공지능 수업을 들은 친구와 이야기를 하다가 생각이 떠올랐다. 원래 한 사람 앉혀놓고 설명하면서 공부하는 스타일. 고맙다 친구야!)

이렇게 그리고 나니 숨통이 트였다. Sigmoid Function으로 만든 Logistic Regression 모델은 3차원 공간에 숨어있었다. 그리고 나의 생각이 맞는지 더 찾아보았다.

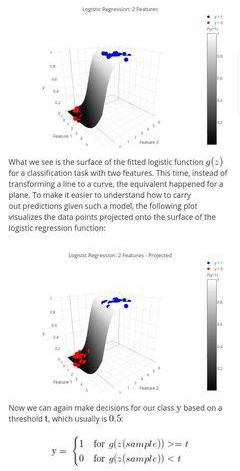
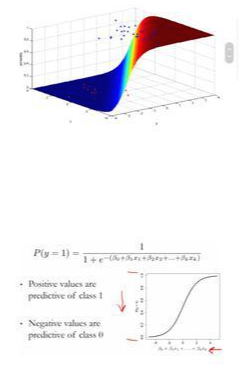
정확하게 일치하는 자료들을 보면서 강의에서는 왜 이런 단계를 건너뛴 걸까..라는 아주 작은 불만도 잠시 떠올랐지만 덕분에 확실히 개념을 잡고 가는 것 같아 뿌듯하다. 공부하면서 사소한 것들이 머릿속에 이미지화되지 않으면 그 부분에서 걸리기 때문에 꼭 실마리를 풀고 가야 한다. 시원해진 속과 따뜻한 머리로 공부에 박차를 가하자!