2020. 11. 11. 23:23ㆍ머신러닝
저번 강의에 이어서

세 개의 다중 분류를 하려고 보니. Binary Classification을 세 번 하면 되니까. 각각의 Label에 대한 가중치를 행렬로 묶어서 한 번에 계산했다.

그래서 각각의 Hypothesis는 하나의 Hypothesis 처럼 보이고. 여기에 어떤 x 값(test set)을 넣으면 우리의 Hypothesis는 A, B, C에 대한 결과 값을 Weight에 따라 벡터의 형태로 출력할 것이다. 근데 우리가 원하는건 그래서 결과가 뭔데?이다. Binary에서는 Sigmoid를 이용해 출력 값을 0~1의 값으로 만들었는데, Multinomial에서는 다른 함수를 사용해서 다수의 출력을 각각 0~1, 합이 1이 되게 만든다.

이를 위한 함수가 Softmax이다.
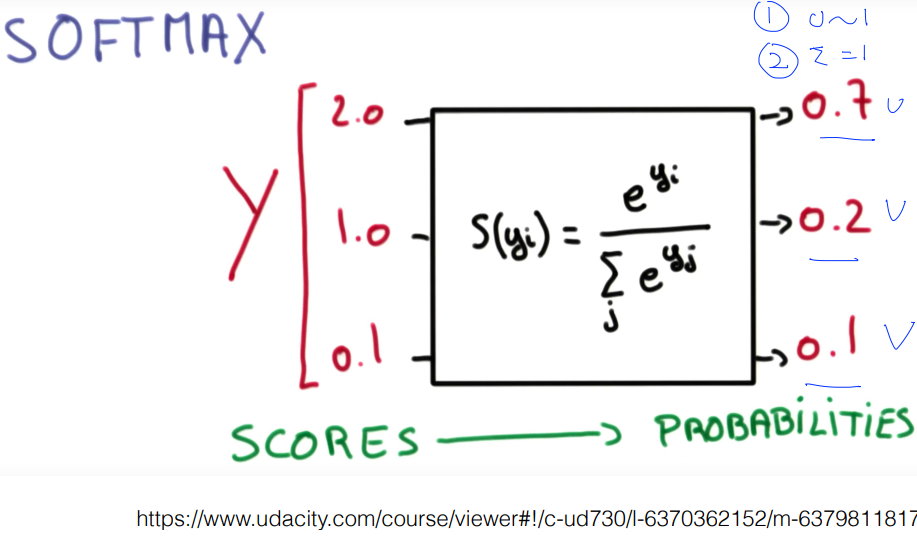
사실 아주 단순하다. n개의 y값들(여기서는 좌측의 Scores)을 다 합한 값에서 하나의 y가 갖는 비율인데. 이게 Probability가 되겠지? 이렇게 우리가 이해하기 매우 쉬운 확률의 모습으로 보여준다.

그래서 뭐냐고! 라고 할 땐 'argmax'라는 함수로 'one-hot encoding'을 해서 가장 높은 확률을 1로 나머지는 0으로 만든다. 그럼 띵! 하고 하나를 보여준다.
(one-hot encoding은 하나만 1이고 나머지는 0인 그룹이다. 반대로 하나만 0이고 나머지는 1이면 one-cold라고 한다.)
이렇게 Multinomial Classifier가 작동하는 과정을 이해했다. 그럼 다음은 이런 Hypothesis(모델, Weight 값들)을 찾기 위해 반드시 설정해야 하는 Cost function을 알아볼 차례이다.
그 전에 Binary classification의 Cost function을 remind 해보자.
y = 1일 때와 0일 때를 나누었었는데,
y = 1인 경우, -log(h(x))
y = 0인 경우, -log(1-h(x)). 두 식을 합치면 C(h(x), y) = -y(log(h(x))-(1-y)(log(1-h(x))였다.
(공부한 지 얼마나 됐다고 곧바로 안 나오네)
Cross-Entropy라는 방식인데,

좌측(S)은 Softmax를 통해 우리가 얻은 값 = 예측값(H(x)) = y bar. 우측(L)은 Label 값 = y이다. Classification에서는 위에서 복습한 것처럼. Log를 이용해서 우리가 원하는 cost function을 만들었다. 예측값과 정답이 완전히 다르면 무한대의 Loss를 주고, 같으면 0의 Loss를 주는 극단적인 Cost function. 위의 Cross-entropy도 같아 보인다. 어차피 L 값은 1 또는 0이고. S값은 1~0의 값이니. 예측 값이 정답에 가까워질수록 Loss는 0에 가까울 것이다.


정답이 Y = [0]
[1] = B 일 때의 경우의 수

정답이 Y = [1]
[0] = A 일 때의 경우의 수. 생각한 대로 전개된다.

Logistic cost와 Cross entropy가 같은 이유는 위에서 이미 말했다.

Traing Set가 하나일 리는 거의 없을 텐데, Training Set의 수로 평균을 내주면 되겠다.

그렇게 나온 Cost function을 Gradient descent를 통해 Weight matrix를 찾아내면 된다. 끝~
'머신러닝' 카테고리의 다른 글
| [텐서플로우로 시작하는 딥러닝 기초] Lab 06-2: Fancy Softmax classifier 를 TensorFlow 로 구현하기 (0) | 2020.12.22 |
|---|---|
| [텐서플로우로 시작하는 딥러닝 기초] Lab 06-1: Softmax classifier 를 TensorFlow 로 구현하기 (0) | 2020.12.05 |
| [텐서플로우로 시작하는 딥러닝 기초] Lec 06-1: Softmax Regression: 기본 개념소개 (0) | 2020.10.29 |
| [텐서플로우로 시작하는 딥러닝 기초] 복습과 고민 (0) | 2020.10.17 |
| [텐서플로우로 시작하는 딥러닝 기초] Lec 05-2: Logistic Regression/Classification 의 cost 함수, 최소화 (0) | 2020.09.07 |