2020. 12. 22. 23:26ㆍ머신러닝
Cost함수(Cross entropy)를
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1)로 작성할 수 있지만 내장 함수를 통해
cost_i = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=Y_one_hot)
cost = tf.reduce_mean(cost_i)로 작성할 수 도 있다고 한다.
tf.one_hot 하면 depth 만큼의 열을 갖는 매트릭스로 입력받은 값들의 인덱스에 one-hot을 해준다. 이때 depth의 크기만큼의 행을 갖는 차원이 추가 되기 때문에 겉에 불필요한 차원이 생긴다.
이를 tf.reshape로 없애준다. tf.reshape(-1,depth) 는 최하위 차원의 크기를 depth로 고정하고 나머지 값을 채워주므로 겉의 차원을 깎아준다.
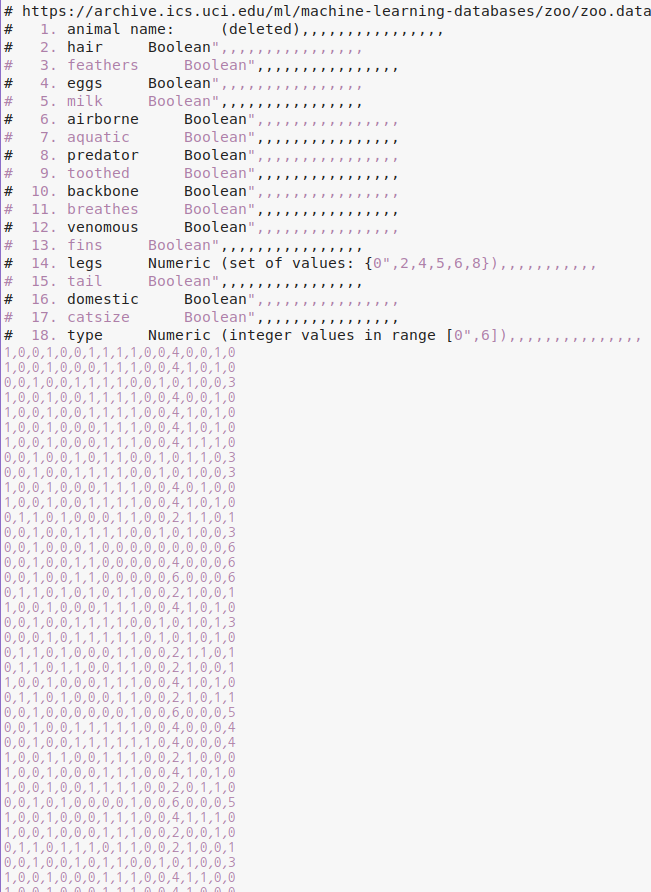
이번에는 데이타를 받아서 다항분류를 해본다.
대충 이렇게 생긴 동물들에 대한 (101, 17) 크기의 matrix다. 0~16 열은 x, 마지막 열은 y이다.
import tensorflow as tf
import numpy as np
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1] #x_data는 (101, 0~16)으로 자르고
y_data = xy[:, -1] #y_data는 (101, 17)로 slice
nb_classes = 7 # 0 ~ 6
# Make Y data as onehot shape
Y_one_hot = tf.one_hot(y_data, nb_classes)
Y_one_hot = tf.reshape(Y_one_hot,[-1, nb_classes])
print(x_data.shape, Y_one_hot.shape) #(101, 16) (101, 7)
#Weight and bias setting
W = tf.Variable(tf.random.normal([16, nb_classes]), name='weight')
b = tf.Variable(tf.random.normal([nb_classes]), name='bias')
variables = [W, b]# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
def logit_fn(X):
return tf.matmul(X, W) + b
def hypothesis(X):
return tf.nn.softmax(logit_fn(X))
def cost_fn(X, Y):
logits = logit_fn(X)
cost_i = tf.keras.losses.categorical_crossentropy(y_true=Y, y_pred=logits,
from_logits=True)
cost = tf.reduce_mean(cost_i)
return cost
def grad_fn(X, Y):
with tf.GradientTape() as tape:
loss = cost_fn(X, Y)
grads = tape.gradient(loss, variables)
return grads
cost_fn 에 보면 tf.keras.losses.categorical_crossentropy 함수로 cross entropy를 해준다. 뒤에 보면 from_logits가 있는데 여기서 말하는 logit이 뭘까? 여기에서는 단순하게 입력값이 Sigmoid나 Softmax 처럼 한정된 범위로 normalization 되었느냐 를 뜻한다. 범위가 [-inf,inf] 인 함수를 logit 이라 하면 될 것 같다. 보면 hypothesis에서는 tf.nn.softmax를 통해 normalization 해주었는데 이를 사용하지 않고 logits, 즉 logit_fn(X)을 사용했으므로 from_logits = True로 입력했다. 자세한 내용은 아래 링크에서 참고.
stackoverflow.com/a/52111173/4334743
What is the meaning of the word logits in TensorFlow?
In the following TensorFlow function, we must feed the activation of artificial neurons in the final layer. That I understand. But I don't understand why it is called logits? Isn't that a mathemati...
stackoverflow.com
prediction이 추가 되었다.
def prediction(X, Y):
pred = tf.argmax(hypothesis(X), 1)
correct_prediction = tf.equal(pred, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
return accuracysoftmax를 거친 hypothesis(X)를 이용해서 예측값을 구하고 이를 정답과 비교해 평균을 낸다.
optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)
for i in range(epochs):
grads = grad_fn(X, Y)
optimizer.apply_gradients(zip(grads, variables))
if (i==0) | ((i+1)%verbose==0):
# print('Loss at epoch %d: %f' %(i+1, cost_fn(X, Y).numpy()))
acc = prediction(X, Y).numpy()
loss = cost_fn(X, Y).numpy()
print('Steps: {} Loss: {}, Acc: {}'.format(i+1, loss, acc))
fit(x_data, Y_one_hot)Steps: 1 Loss: 3.635028839111328, Acc: 0.1683168262243271
Steps: 100 Loss: 0.5194157958030701, Acc: 0.7920792102813721
Steps: 200 Loss: 0.31850090622901917, Acc: 0.9108911156654358
Steps: 300 Loss: 0.23534879088401794, Acc: 0.9405940771102905
Steps: 400 Loss: 0.1887214034795761, Acc: 0.9504950642585754
Steps: 500 Loss: 0.158460333943367, Acc: 0.9504950642585754
Steps: 600 Loss: 0.13703754544258118, Acc: 0.9900990128517151
Steps: 700 Loss: 0.12098979949951172, Acc: 0.9900990128517151
Steps: 800 Loss: 0.10847963392734528, Acc: 1.0
Steps: 900 Loss: 0.09843038767576218, Acc: 1.0 Steps: 1000 Loss: 0.09016558527946472, Acc: 1.0
'머신러닝' 카테고리의 다른 글
| [텐서플로우로 시작하는 딥러닝 기초] Lab 07-1: Application & Tips: 학습률(Learning Rate)과 데이터 전처리(Data Preprocessing) (0) | 2020.12.27 |
|---|---|
| [텐서플로우로 시작하는 딥러닝 기초] Lab 06-1: Softmax classifier 를 TensorFlow 로 구현하기 (0) | 2020.12.05 |
| [텐서플로우로 시작하는 딥러닝 기초] Lec 06-2: Softmax Classifier의 cost함수 (0) | 2020.11.11 |
| [텐서플로우로 시작하는 딥러닝 기초] Lec 06-1: Softmax Regression: 기본 개념소개 (0) | 2020.10.29 |
| [텐서플로우로 시작하는 딥러닝 기초] 복습과 고민 (0) | 2020.10.17 |